The Hidden Order in a Poker Chip Shuffle

Idle hands, advanced math

The Gentleman’s Arsenal

Over the years I’ve taught myself a number of moderately impressive but largely unnecessary skills—juggling, yo-yo tricks, knitting, latte art, rope splicing, tying fishing flies. Most recently? Shuffling poker chips like a Vegas card shark. Little did I know that this seemingly idle habit would take me on an unexpected journey to some obscure, and fun, branches of mathematics.

The Stack and the Shuffle

If you, like me, have watched videos of poker tournaments, you've noticed the absentminded way that most of the players shuffle their chips with one hand. I thought it looked cool, and it turns out that it’s not that hard to learn.

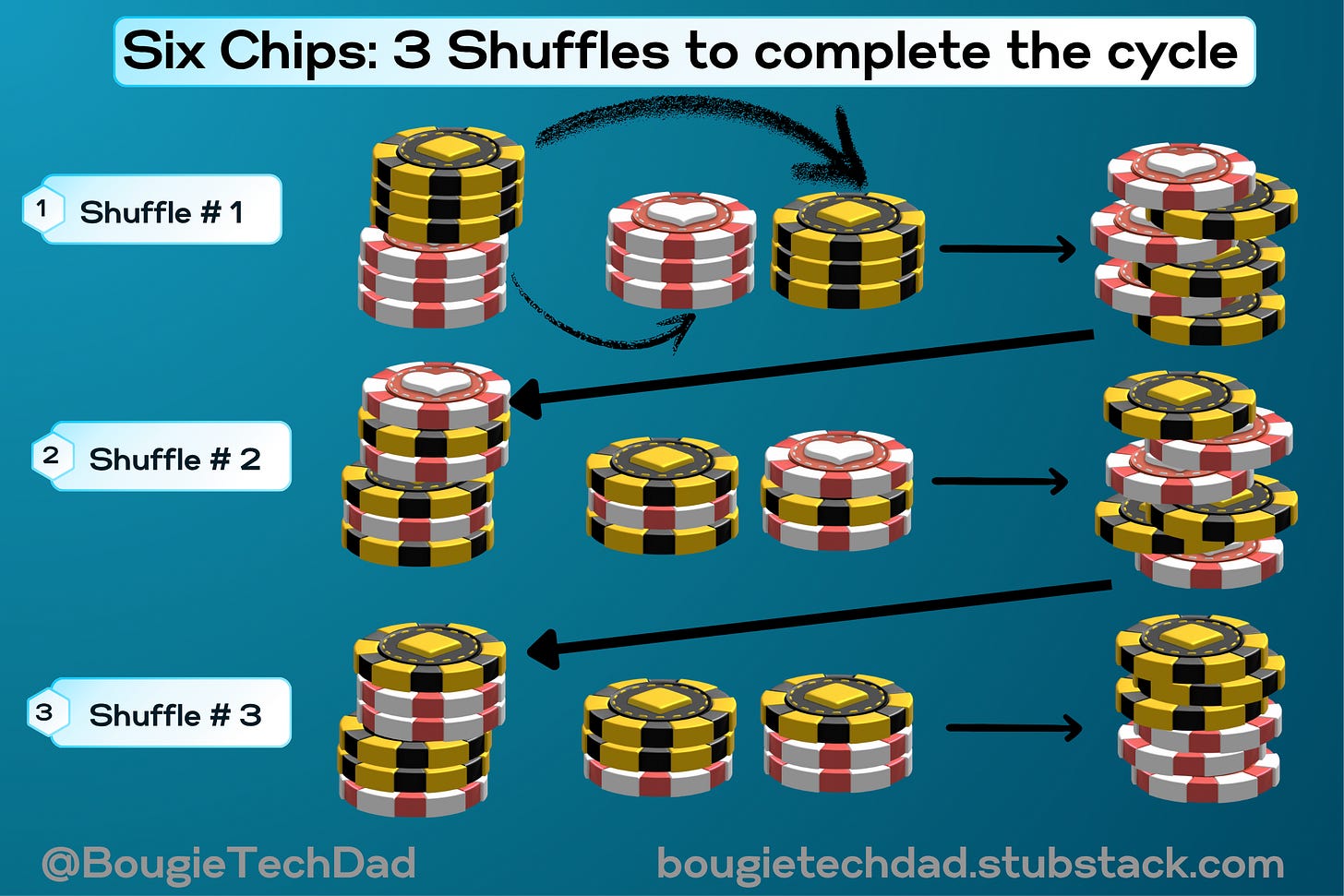
Start with a stack of chips (an even number). I recommend starting small—6 chips. You split the stack in two and, with a one-handed flick (it takes some practice), interleave them back together. Then you split it again—top half to the right, bottom to the left—and start the process over.

Credit: Giphy

In order to check that I was doing a clean shuffle, I used chips of two colors, which allowed me to see if I was properly interleaving the chips. And as I repeated the shuffle, I noticed that—as long as I was doing the shuffle correctly—eventually the chips would return to their original half-and-half order. For six chips, it took only three shuffles to get back to the beginning.

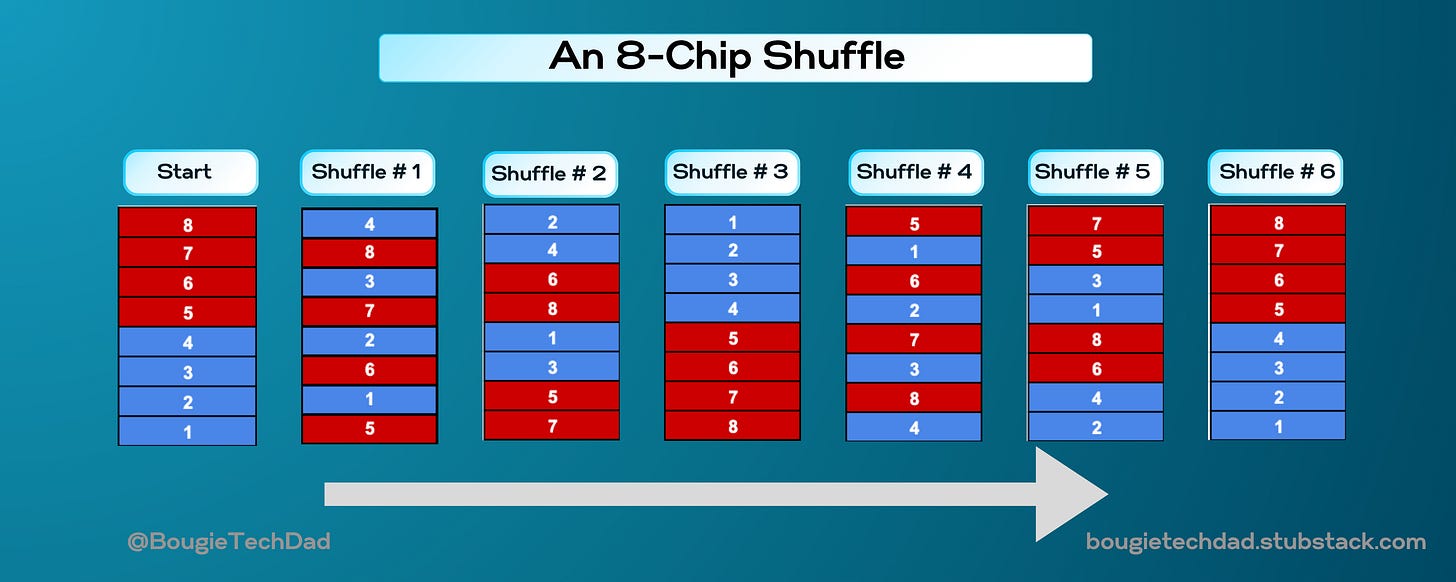
I then tried it out with eight chips. I stacked them up, made 3 careful shuffles, and the colors were again grouped together. Huh? How was it possible that three shuffles produced the same result for different numbers of chips? A tickle started in the back of my brain, leading me to wonder: what are the rules that determine all of this, and is there any predictability to that number?

The answer, as it turns out, is... weird.

Credit: Bougie Tech Dad

A Pattern Emerges

Six chips…three shuffles to complete the cycle. Eight chips…also three shuffles. Or so I thought, until I looked closer, and realized I was wrong.

For a stack of eight chips (four yellow, four white), three shuffles only got me half way. Yes, the yellow and white chips were nicely grouped together. But once I paid more attention, I saw that I wasn't quite back at the beginning state. Unlike in the 6-chip example, the four white chips (which had started on the bottom of the stack) were now on top after three shuffles. Was looking at groups of color enough? I probably needed to look at individual chips.

To really figure this thing out, I manually numbered the chips 1 through 8 and recording each step on paper. Taking the time to sketch it out by hand helped me to see how individual chips cycled to new positions in the stack.

As the picture became clearer, I realized my mistake: while the colors had returned to their original grouping after three shuffles, the individual chips hadn’t gotten back to their original order. Their positions were wrong. They were perfectly reversed. Visually convincing, mathematically false.

Working it out by hand slowed things down and gave me a chance to appreciate the dance that was happening before me. Groups of colors formed in one shuffle and disappeared in the next. Sometimes the odd- and even-numbered chips clustered together for a bit, before morphing into something completely different. What I was seeing was beautiful, and I was getting glimpses of the rules that were at work. But I could only do so much with pen, paper, and physical chips.

After shuffle #3, the chips have perfectly reversed order. But it takes six shuffles to complete the cycle. Credit: Bougie Tech Dad

Calling for Backup

Sketching manually had slowed things down enough to reveal some of the patterns of the process, but it was also time-consuming and prone to errors as the number of chips increased. I knew there was a structure here. Something mathematical. Something about transformations? Permutations, maybe?

In addition to spending time researching, I also asked GenAI to build me a script that would run simulations. My prompt¹ outlined the shuffle: total number of chips, number of colors, etc. It described the general setup, the shuffling rules, the way I’d been tracking chip positions. I even explored—very briefly, and via a script—what would happen if the stack were split into three or four piles before shuffling. Not very realistic, I'll admit, but fun to use as a point of exploration. (And if anyone manages to master a one-handed shuffle of 3 stacks of chips I'll buy them a beer.)

Systems Beneath the Surface

My research hit paydirt: I seemed to have stumbled into a subset of algebra called group theory. And my poker chip shuffling was a deterministic permutation of chip positions, repeated over time.

I won't go into all the gory mathematical detail here. That part will live in a footnote² for the curious. The point I really want to make is that—like most things in this world—what could easily be mistaken for a bunch of randomness was actually a lovely ballet, driven by a knowable process. Lying just below the surface of the chip shuffle was a system—and a pretty complex one at that—that was running the show.

Systems Thinking in the Smallest Things

So yes: a post about poker chips. But also a post about how systems are everywhere, and how powerful it can be to let intuition and curiosity run their course. Curiosity is a muscle. Pattern recognition is a skill. Answers to a question just for the joy of it can be their own reward.

And the next time you find yourself idly fidgeting, maybe you will see that it’s actually an investigation. You might be one shuffle, one flick, or one spin away from uncovering a hidden universe hiding in plain sight.

---

The Numbers:

Bougie Factor: 🎩🎩🎩 (Turning idle play into an abstract algebra demo? Very on-brand.)

Tech Factor: ⚡⚡ (Medium tech, but deeply nerdy research. Bonus lightning bolt for pairing manual sketching with code-based simulation.)

Is it worth it?: 💰💰💰 (It won’t make dinner faster or save you money. But there’s value in taking time to discover hidden complexity in the world.)

---

Footnotes:

1. The prompt I used with GenAI:

I'm playing around with shuffling poker chips, and observing how they shift around in order. I'm not a mathematician or a cryptographer, but i feels to me like there must be some formula that defines how the chips change position through the stack of chips after each shuffle. It feels like 'transformation' might be a formal word to describe the changing order of the chips after each shuffle. I've been modeling this manually, with stacks of increasing numbers of chips. But it becomes laborious as the number of chips gets higher. Can you help me model this out? Here are the parameters of the shuffling transformation. I have been using equal numbers of yellow and white chips, because it's easy for me, visually, to see what happens. But we don't have to do it that way.

1) Let's assume we always use an even number of chips (N). Split the chips into two stacks. One on the right and one on the left

2) Shuffle them as follows: The bottom chip on the right stack is placed first. Then the bottom chip on the left stack. Then the second chip from the bottom of the right stack, and then the second chip from the bottom of the left stack, and so on until all of the chips are in one new stack 

3) Take the top half of the stack and place it to the right. So we now have two new stacks, right and left

4) Shuffle again per step 2 

5) Split again per step 3 

6) Repeat steps 4 and 5 until the chips return to their original configuration 

Can you write a script that replicates this process? I'd like to see how many shuffles it takes to run a stack of 6, 8, 10, 12 chips through the transformations and return it to the original configuration. Thanks!

Footnote: The Math Beneath the Shuffle

2. What I found in this exploration is a beautiful corner of mathematics called permutation cycles within group theory. Here's the high-level version of what’s happening under the hood:

The Shuffle as a Permutation

Each shuffle rearranges the stack in a very specific, repeatable way. In math terms, it’s a deterministic permutation of the chips' positions. If you label the chip positions starting from the bottom (position 0) to the top (position N-1), the shuffle can be written as a function that moves each chip to a new position.

For example, after one shuffle:

• The chip in position 0 might move to position 3.

• The chip in position 3 might move to position 1.

• The chip in position 1 might move back to position 0.

This is what’s known as a cycle: the chips in positions 0 → 3 → 1 → 0 rotate among themselves. They form a closed loop.

Multiple Cycles

The stack can break into multiple independent cycles. For example:

• Chip 0 might follow a cycle through positions 0 → 3 → 1 → 0.

• Chip 2 might move through positions 2 → 5 → 4 → 2.

Each of these cycles operates independently but they all have to return to their starting positions to fully "reset" the stack.

The Order of the Permutation

The order of a permutation is the number of shuffles required to return the stack to its exact starting configuration. Mathematically, it’s calculated as the least common multiple (LCM) of the lengths of all the cycles.

For example:

• If the cycles are [3, 3], the order is LCM(3, 3) = 3.

• If the cycles are [4, 2], the order is LCM(4, 2) = 4.

This explains why some stack sizes (like 6 chips) reset more quickly than others, and why the shuffle cycle length doesn’t grow in a simple, predictable way with the number of chips.

Here’s how some of the numbers work out as more chips are used:

Number of Chips | Shuffles to Complete Cycle
6               | 3
8               | 6
10              | 12
12              | 10
14              | 4
16              | 8
18              | 8
20              | 18
22              | 6
24              | 22

Why It’s Cool

This works for shuffling poker chips, and it’s the same math that governs the way Rubik’s Cubes reset, how cryptographic systems shuffle data, and how many shuffle operations are needed to randomize a deck of cards.

If you want to go deeper, follow those links above to topics like "permutation cycles" and "group theory" and think about them in the context of the symmetric group (Sₙ). You’ll find this little poker chip shuffle sitting comfortably alongside some of the most powerful mathematical ideas in modern systems.

I also recommend reading about the Solitaire Cypher (also called ‘Pontifex’) from the novel Cryptonomicon by Neal Stephenson, which is a cryptographic cypher done using a very careful shuffling of a deck of cards.